பென்ஃபோர்டின் சட்டம் என்றால் என்ன? ஏன் இந்த எதிர்பாராத எண்களின் முறை எல்லா இடங்களிலும் உள்ளது

நபர்களின் நல்ல நண்பர் எண்ணிக்கை 1 அல்லது 2ல் தொடங்கும் போது, ​​அற்பமான 10 சதவீதம் பேர் 8 அல்லது 9ல் தொடங்கும் போது அதிக ஏற்றத்தாழ்வைக் காணலாம். இதை நினைவில் கொள்ளுங்கள். அதிகமாகவோ அல்லது குறைவாகவோ நண்பர்களைக் கொண்டிருப்பது அல்ல: 1,000 நண்பர்களை வைத்திருப்பது 8ஐக் காட்டிலும் மேலானது.

இந்த வினோதமான 1கள் மற்றும் 2களின் பிரதிநிதித்துவம் நல்ல நண்பர்கள் மற்றும் ரசிகர்களுக்கு அப்பால் விருப்பங்கள் மற்றும் மறு ட்வீட்கள் வரை நீண்டுள்ளது, மற்றும் கணித உலகின் பல மூலைகளிலும் சமூக ஊடகங்களுக்கு அப்பால்: நாட்டின் மக்கள்தொகை, ஆற்றின் நீளம், மலை உயரங்கள், இறப்பு விகிதம், பங்குச் செலவுகள், அறிவியல் அமெரிக்கன் என்ற சாதாரண கவலையில் கண்டுபிடிக்கப்பட்ட பல்வேறு எண்களின் தொகுப்பு கூட . சிறியதாக மாற்றப்பட்ட முன்னணி இலக்கங்கள் மிகவும் பொதுவானவை அல்ல, இருப்பினும் அவை துல்லியமான மற்றும் நிலையான வடிவத்தைப் பின்பற்றுகின்றன.

அனைத்து இலக்கங்களும் ஒரே மாதிரியாகக் குறிப்பிடப்பட்டால், ஒருவர் அப்பாவியாக எதிர்பார்த்தபடி, அவை ஒவ்வொன்றும் ஒன்று தோன்றும். ஒன்பதாவது (சுமார் 11.1 சதவீதம்) நேரம். இருப்பினும், குறிப்பிடத்தக்க எண்ணிக்கையிலான நிஜ-உலகத் தகவல் தொகுப்புகளில், ஈர்க்கக்கூடிய 30.1 சதவீத உள்ளீடுகள் 1, 17.6 சதவீதம் தொடக்கம் 2, மற்றும் பல. இந்த நிகழ்வு பென்ஃபோர்டின் விதியாக புரிந்து கொள்ளப்படுகிறது. உங்கள் தகவலின் அமைப்புகளை நீங்கள் மாற்றியமைக்கும் போதும் சட்டம் தொடர்கிறது. ஆறுகளை அடி அல்லது பர்லாங்குகளில் அளவிடவும், டாலர்கள் அல்லது தினார்களில் படி பங்கு விலைகள், எந்த முறையிலும் நீங்கள் தீர்மானிக்கும், இந்த குறிப்பிட்ட சதவீத முன்னணி இலக்கங்கள் உறுதியாக இருக்கும். கணிதவியலாளர்கள் உண்மையில் பல ஆக்கப்பூர்வமான காரணிகளை முன்மொழிந்துள்ள நிலையில், அதன் முழுமையான உலகளாவிய தன்மை ஒரு அடிப்படை விளக்கத்தைத் தவிர்க்கிறது.

இது ஒரு மிதமான கவனிப்பு போல் தோன்றலாம், இருப்பினும் பென்ஃபோர்டின் சட்டம் தனிநபர்களை கம்பிகளுக்குப் பின்னால் நிறுத்துவதற்கும் மோசடிகளின் மகத்தான செயல்பாடுகளைக் கண்டறிவதற்கும் பயனுள்ள தாக்கத்திற்குப் பயன்படுத்தப்பட்டது.

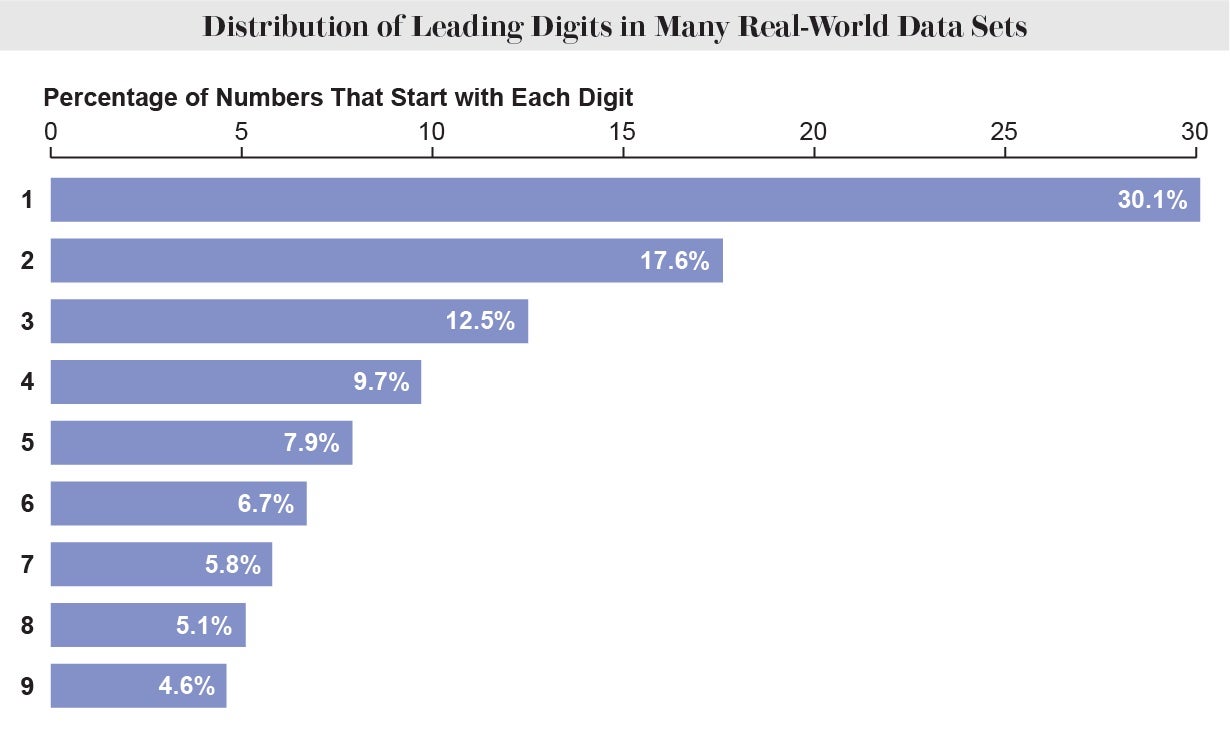
கடன்: Amanda Montañez; ஆதாரம்: “இயற்கை எண்களில் வெவ்வேறு இலக்கங்களின் பயன்பாட்டின் அதிர்வெண் பற்றிய குறிப்பு,” சைமன் நியூகாம்ப் அமெரிக்கன் ஜர்னல் ஆஃப் மேதமேடிக்ஸ் , தொகுதி. 4, எண். 1; 1881 (தரவு)

கால்குலேட்டர்களுக்கு முன், தனிநபர்கள் மடக்கை அட்டவணைகள் எனப்படும் பரிந்துரை புத்தகங்களுக்கு ஹேரி கணிதத்தை அவுட்சோர்ஸ் செய்தனர். 1881 ஆம் ஆண்டில், வானியலாளர் சைமன் நியூகாம்ப், மடக்கை அட்டவணைகளின் ஆரம்பப் பக்கங்கள், ஒன்றிலிருந்து தொடங்கும் எண்களுக்கு ஒத்ததாக இருப்பதைக் கண்டார், மேலும் அழகான பின் பக்கங்களுடன் ஒப்பிடும்போது அவை பயன்படுத்தப்பட்டன. இயற்கையான தகவல் தொகுப்புகளில் சிறியதாக இருக்கும் முன்னணி இலக்கங்கள் மிகவும் பொதுவானதாக இருக்க வேண்டும் என்று அவர் கண்டறிந்தார், மேலும் அவர் சரியான பகுதிகளை வெளியிட்டார். இயற்பியலாளர் ஃபிராங்க் பென்ஃபோர்ட் 1938 இல் இதேபோன்ற அவதானிப்பை மேற்கொண்டார் மற்றும் சட்டத்தை மேம்படுத்தினார், அதன் உலகளாவிய தன்மையைக் காட்ட 20,000 க்கும் மேற்பட்ட தகவல் புள்ளிகளைச் சேகரித்தார். திசைதிருப்பல்: பென்ஃபோர்டின் பெயரிடப்பட்ட கடன் என்பது ஸ்டிக்லரின் சட்டத்தின் ஒரு சூழ்நிலையாகும், இது மருத்துவ கண்டுபிடிப்புகள் ஒருபோதும் அவற்றின் ஆரம்ப கண்டுபிடிப்பாளர் என்று அழைக்கப்படுவதில்லை. ஸ்டிக்லரின் சட்டம் சமூகவியலாளர் ராபர்ட் கே. மெர்ட்டனால் வலியுறுத்தப்பட்டது, அதற்கு முன்பு ஸ்டீபன் ஸ்டிக்லர் தனது பெயரைப் பெற்றார்.

பென்ஃபோர்டின் சட்டம் வெறுமனே ஒரு பகுப்பாய்வு ஆர்வம் அல்ல: பணவியல் ஆலோசகர் வெஸ்லி ரோட்ஸ், நிதியாளர்களை ஏமாற்றிய குற்றச்சாட்டில், மாவட்ட வழக்கறிஞர்கள் நீதிமன்றத்தில் வாதிட்டபோது, ​​அவரது கோப்புகள் முன்னணி இலக்கங்களின் எதிர்பார்க்கப்பட்ட புழக்கத்திற்கு இணங்கவில்லை. மேலும் அவை துரோகத்திற்காக உருவாக்கப்பட்டிருக்கலாம். கான்செப்ட் லேட்டரான் அசிஸ்டெட் கம்ப்யூட்டர் சிஸ்டம் ஆராய்ச்சியாளர் ஜெனிஃபர் கோல்பெக் ட்விட்டரில் ரஷ்ய போட் நெட்வொர்க்கைக் கண்டுபிடித்தார். பெரும்பாலான பயனர்களுக்கு, அவர்களது ரசிகர்கள் பென்ஃபோர்டின் சட்டத்தை கடைபிடிக்கும் ரசிகர்களின் எண்ணிக்கையை அவர் கவனித்தார், இருப்பினும் செயற்கைக் கணக்குகள் முறையிலிருந்து கணிசமாக திசைதிருப்பப்படுகின்றன. போலி ரீட்வீட்களை வாங்கும் நபர்களைப் பிடிக்க அவர் ஒப்பிடக்கூடிய நுட்பங்களைப் பயன்படுத்தினார். மோசடிகளைக் கண்டறிவதற்குப் பயன்படுத்தப்படும் பென்ஃபோர்டின் சட்டத்தின் எடுத்துக்காட்டுகள் ஏராளமாக உள்ளன, மேக்ரோ பொருளாதாரத் தகவலைக் கட்டுப்படுத்தும் கிரேக்கத்திலிருந்து i